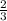Для каких значений а и в вершиной данной параболы есть точка а(1; 1/3) у=ах2+вх-1
Другие вопросы по теме Алгебра
Популярные вопросы
- 10-15 предложений. Почему после прочтения рассказов Шукшина чудик , микроскоп ,...
1 - Реши примеры . 18 · (5 · 7) 35 · (2 · 6) (3 · 10) · 19 15 · 16 25 · (9 · 4) 36...
2 - Два различных числа, расположенных на одинаковом расстоянии от начала отсчета на...
1 - в тільки напишіть розповідь про гетьмана Івана Мазепу (5-7 речень)...
3 - … pupils in our class know English. So they don’t understand what the teacher says....
2 - Який об’єм водню виділиться при взаємодії оцтової кислоти з 2 моль кальцію? ...
2 - По количеству морфологический разбор...
1 - сколько видов влегкой атлетике, название этих видов...
3 - Дана точка М (2; 3). Определите координаты точек симметричных точке М.В – относительно...
2 - Реагирует ли метилбензол с азотом?...
2
Подставляя координаты точки А (1;1/3), получаем уравнение:
а+в-1=1/3
Абсцисса вершины параболы определяется по формуле х=-в/(2а), в нашем случае:
-в/(2а) = 1
Из первого уравнения выражаем в и подставляем во второе:
в=-2а
а-2а-1=1/3
-а = 1 1/3
а = -1 1/3
в = -2*(-1 1/3) = 2 2/3
ответ: а=-1 1/3; в=2 2/3
1) A(x;y) в нашем случаи x=1, a y=1/3
подставим эти значения в урав. параболы:
отсюда получим
3a+3b=4
2) Возьмем производную от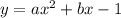
(y)'=2ax+b
3) теперь подставим x=1 и приравняем выражение к 0
0=2a+b
4) Теперь необходимо решить систему 2-ух линейных уравнений.
Решив систему получим a=-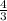 и b=
и b=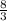
в совершенном виде a=-1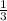 и b=2
и b=2