1. Алгебра
  2. Для графика квадратичной функций

Для графика квадратичной функций y=-x^2+6x-3 найдите 1)ось симметрий 2)промежуток возрастания ,убывания 3)наибольшие значение функций 4)множество значений функций 5) расстояние от вершины параболы до начальной координаты по возможности распишите

VafaMurad VafaMurad    1   14.03.2019 22:58    3

Ответы
NazSha NazSha  25.05.2020 10:55

y=-x^2+6x-3

1) Ось симметрии проходит через вершину параболы, параллельно оси ОУ. Абсцисса вершины равна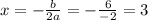  x=-\frac{b}{2a}=-\frac{6}{-2}=3  .

Уравнение оси симметрии: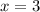  x=3  .

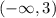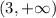2)  Так как ветви параболы направлены вниз (а=-1<0), то промежуток возрастания  (-\infty ,3)  , а промежуток убывания  (3,+\infty ) .

3) Наибольшее значение функция принимает в своей вершине:

y(3)=-3^2+6\cdot 3-3=-9+18-3=6

4)  Множество значений функции:  y\in (-\infty ,6\, ] .

5)  Расстояние от вершины параболы до начала координат равно

d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(3-0)^2+(6-0)^2}=\sqrt{9+18}=\\\\=\sqrt{27}=\sqrt{9\cdot 3}=3\sqrt3


Для графика квадратичной функций y=-x^2+6x-3 найдите 1)ось симметрий 2)промежуток возрастания ,убыва
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ulyana1512200214 ulyana1512200214  05.05.2021 20:33
. 7 задание егэ. я не понимаю почему ответ 7, а не -7. объясните по-русски, умоляю всей душой​...
Эмиль2330 Эмиль2330  05.05.2021 20:32
можно ли айпад аир 2020 подключить к мэджик кейборд , а то не знаю есть ли клава мэджик кейборд на аир 2020!...
kerimbaevazarema03 kerimbaevazarema03  05.05.2021 20:32
Сумма корней квадратного уравнения х квадрат-7х+3...
uchenica7 uchenica7  05.05.2021 20:32
7. Найдите для функции у=-5/х а) область определения функцииб) множество значений функции:в) промежутки знакопостоянства функции;г) промежутки монотонности функции.​...
ivanovasvetak ivanovasvetak  11.06.2019 19:30
Вклассе 30 учеников. 11/15 всего класса приняли участие в туристическом походе походе. сколько учеников было в походе?...
rewington1 rewington1  11.06.2019 19:30
Втрех классах всего 119 учащихся. в первом классе на 4 человека больше , чем во втором , и на 3 человека меньше, чем в третьем классе. сколько учащихся в каждом...
Lina300333 Lina300333  11.06.2019 19:30
Построить график функции : у=4 в степени х, у=1/3 в степени х...
ponomarjovakse ponomarjovakse  11.06.2019 19:30
:вынесите множитель из под знака корня. √27. √98. √80. √160. √432. √675....
Anastasias223 Anastasias223  11.06.2019 19:30
вас,! раскройте скобки и подобные слагаемые: 6(х-1,+7х)...
HOHOL666 HOHOL666  11.06.2019 19:30
40 найдите множество целых значений x при которых верно неравенство : а) -4...

Популярные вопросы