1. Алгебра
  2. Для функции f(x) = 2x^2+x

Для функции f(x) = 2x^2+x найдите первообразную, график которой проходит через точку а(1; 1)

liteman1000ow7ldr liteman1000ow7ldr    3   17.08.2019 21:10    2

Ответы
афкашник афкашник  05.10.2020 01:32

Общий вид первообразной: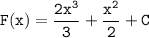 \tt F(x)=\dfrac{2x^3}{3} +\dfrac{x^2}{2} +C, проходящая через точку A(1;1). Подставив координаты точки в общий вид первообразной, получим:

\tt 1=\dfrac{2\cdot1^3}{3} +\dfrac{1^2}{2} +C~~|\cdot 6\\ \\ 6=4+3+6C\\ \\ 6C=-1\\ \\ C=-\dfrac{1}{6}


\boxed{\tt F(x)= \dfrac{2x^3}{3} +\dfrac{x^2}{2}-\frac{1}{6} }

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Syrup75 Syrup75  07.04.2020 11:47
Привет решить все варианты...
08Dasha06 08Dasha06  07.04.2020 11:47
Какие из этих чисел будут решением неравенства - 15 + 4 x a 3-9-110-61205-10​...
sasha123123476 sasha123123476  07.04.2020 11:47
Задание 3.Для каждого значения а решите уравнение,х2+ (1 - 3а)x + 2а даю! ​...
DDaVV DDaVV  07.04.2020 11:47
Із міста А до міста Б виїхали 5 автобусів і 7 рейсів електропотягів. Скількома можна потрапити із міста А до міста Б будь-яким видом транспорту? ​...
duminalarisa duminalarisa  07.04.2020 11:47
Прочитайте текст. Для окраски металлических поверхностей можно пользоваться кистью, малярным валиком или распылителем краски — краскопультом. При окраске кистью...
тууутуууу тууутуууу  07.04.2020 11:46
Мать может прополоть картофель за 1 час, а дочь — за 4 ч. Сколько времени они будут пропалывать картофель, работая одновременно? ответ вырази в минутах. Одновременно...
alesyabogun135 alesyabogun135  07.04.2020 11:46
Решить уравнение X^2-6x =x 3...
dashameluhova95 dashameluhova95  07.04.2020 11:45
Выполните в тетрадях построения графиков следующих функций:y=2x; b) y=-2x; c) y=0,5x; d) y=-0,5xпостроения графиков выполняем в одной системе координат!Подпишите,...
zaqwsxcde zaqwsxcde  07.04.2020 11:43
Вынеси за скобки множитель : - 42zx +56zy - 98z...
Змей19 Змей19  07.04.2020 11:42
Задайте формулою пряму пропорційність, якщо її кутовий коефіцієнт дорівнює середньому арифметичному чисел 3,6 і 12. y- залежна змінна, x-аргумент....

Популярные вопросы