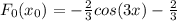Для f(x) =2sin3x найти: а) множество всех первообразных; б) первообразную, график которой проходит через a (п/3; 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужно 15 производных предлогов и 15 наречий от которых произошли...
3 - Мнение о трагичном финале портрет. 15 б....
3 - Напишите эссе на тему эссе- это маленькое сочинение...
2 - Звать через к настоящему, значение ✨...
1 - Почему голосеменные растения образуют большое количество пыльцы?...
2 - Мини доклад на тему золотистые водоросли....
2 - Из подъезда в 8.00 утра вышли два человека. скорость первого 100...
2 - Придумайте мне не большой рассказ,употребляя слова закон,порядок,правонарушения...
2 - Критик михайловский желчно говорил, что чехов изображает все,...
1 - Сколько будет 9,4 умножить на 5, а потом из получившегося вычесть...
2
Сначала найдем множество первообразных. для этого нужно взять интеграл от f(x).
Множество первообразных будет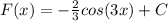
Теперь найдем первообразную, график которой проходит через A (П/3; 0).
Для этого надо решить уравнение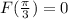 , и найти отсюда C.
, и найти отсюда C.
Решаем:
Нашли C, подставим в уравнение первообразной и получим:
ответ: Множество всех первообразных: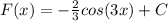
Первообразная, график которой проходит через A (П/3; 0):