1. Алгебра
  2. Дифференциальное уравнение

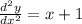
Дифференциальное уравнение \frac{d {}^{2}y }{d {x}^{2} } = x + 1 \: \: \: \: \: \: \: \:
при y=2 x=0. и y=1 x=2

SilvAqualius SilvAqualius    3   30.12.2021 15:20    1

Ответы
nadj5555 nadj5555  15.02.2022 01:20

\dfrac{d^2y}{dx^2} =x+1

Сначала найдем общее решение уравнения:

y''=x+1

y'=\int(x+1)dx

y'=\dfrac{x^2}{2} +x+C_1

y=\int\left(\dfrac{x^2}{2} +x+C_1\right)dx

y=\dfrac{1}{2}\cdot\dfrac{x^3}{3} +\dfrac{x^2}{2} +C_1x+C_2

y=\dfrac{x^3}{6} +\dfrac{x^2}{2} +C_1x+C_2

Рассмотрим начальное условие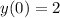 y(0)=2:

2=\dfrac{0^3}{6} +\dfrac{0^2}{2} +C_1\cdot0+C_2

C_2=2

Общее решение принимает вид:

y=\dfrac{x^3}{6} +\dfrac{x^2}{2} +C_1x+2

Рассмотрим начальное условие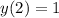 y(2)=1:

1=\dfrac{2^3}{6} +\dfrac{2^2}{2} +C_1\cdot2+2

1=\dfrac{4}{3} +2 +2C_1+2

3=4+6 +6C_1+6

6C_1=3-4-6-6

6C_1=-13

C_1=-\dfrac{13}{6}

Значит, частное решение имеет вид:

\boxed{y=\dfrac{x^3}{6} +\dfrac{x^2}{2} -\dfrac{13}{6} x+2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
DjDenZzz DjDenZzz  12.05.2021 19:11
Найдите решение системы уравнений:​...
loric225p0cgrp loric225p0cgrp  12.05.2021 19:11
Объясните решение систем уравнение с сложения​...
ygthjkujny ygthjkujny  12.05.2021 19:11
ОЧЕНЬ НУЖНО: Точка d равноудалена от точек a и b.Точка e равноудалена от точек b и c.Угол bad=40 градусов,угол bce=60 градусов.Найдите углы треугольника dbe...
Nataliaroy Nataliaroy  12.05.2021 19:11
Проблема с тригонометрией, Хотя бы один или два номера....
alegarxih alegarxih  12.05.2021 19:12
перший пішохід пройшов 6 км а другий пішохід пройшов 5 км швидкість пішохода на 1 км в годину менше швидкості другого Знайди швидкість пішохода якщо відомо що він був в дорозі на 30...
Марянян Марянян  12.05.2021 19:13
Знайдіть найбільше і найменше значення функції​...
Albina7890 Albina7890  12.05.2021 19:14
Решите abobus abobus abobus abobus abobus abobus abobus abobus abobus abobus abobus abobus abobus...
ak9512 ak9512  26.04.2020 20:17
Нужно найти производную первого порядка...
modinn112 modinn112  26.04.2020 20:17
.У выражение: а). -2xy2 ∙3x3 y5; б). (-4a b3)2 ; в). 2x(2x+3y) - (x+y)2 ;...
kooyrina582mari kooyrina582mari  26.04.2020 20:17
Вместо * поставьте знак или так, чтобы было верным утверждение: если а -5, то -5*а; если -2 а и а b,то -2*а.​...

Популярные вопросы