Дифференциальное уравнение
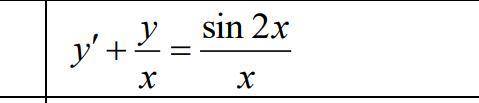
Другие вопросы по теме Алгебра
Популярные вопросы
- Чудесное превращение слов. замени один звук другим и напиши новые слова...
3 - Сделать фонетический разбор слова пальто...
3 - Выручайте! fill the gaps with speak say tell. use them in the correct...
2 - Вспортивном клубе проходит первенство по теннису. проигравший партию...
3 - Оцените политико- положение республики беларусь(выгодно не выгодно)...
2 - Что такое торговые компании , монополио , биржа , капитал , капиталист...
2 - Что осуждает басня ,,листы и корни что высмеивает?...
2 - Участник международного конкурса кенгуру решил 5/8 общего количества...
3 - Написать сочинение по на тему мой первый день в школе . 10 класс. (в...
2 - Как сделать так,чтобы человек в своей стране не чувствовал себя униженным...
1
Это ЛДУ.
Замена:
общее решение