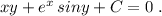Дифференциальное уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Чем можно объяснить высокую эффективность применения приемов устранения...
3 - Бұқаралық ақпарат құралдарының адам өміріндегі маңызы бар ма эссе...
3 - Влияние влажности воздуха на пробивное напряжение в радиочастотном диапозоне?...
3 - В задании нужно вписать слова которые ю предоставлены снизу...
3 - Контрольный тест 11 класс по белорусскому языку Может у кого ответы...
1 - Выберите неверное утверждение: Через любые две точки плоскости проходит...
1 - Сколько энергии тратит динамик, если его сопротивление 8 Ом, а мощность...
2 - Можете придумать девиз к отряду в лагере Телепузики . Даю 100...
2 - Ребята можете мне. варианты: а;б;в;г;д....
2 - Знайдіть середнє арифметичне чисел1,35 я буду вдячна...
3
Проверим, является ли это ДУ уравнением в полных дифференциалах:
Заданное ДУ является уравнением в полных дифференциалах и имеет вид: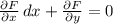 .
.
Oтвет: общий интеграл