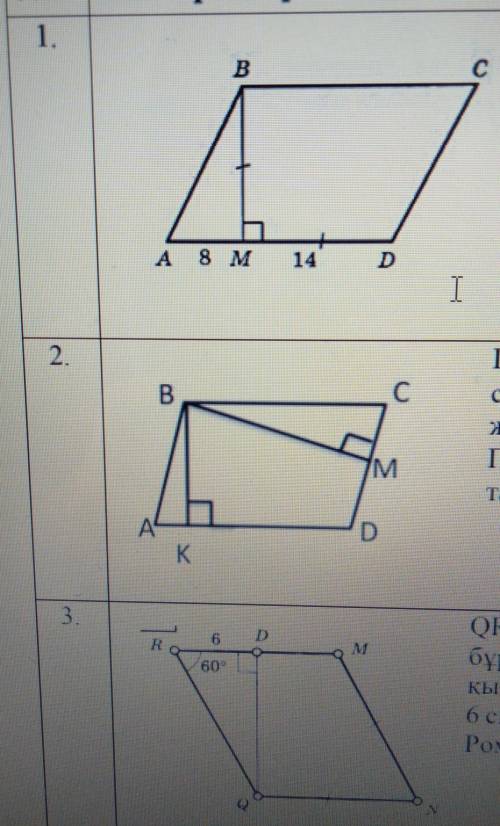
ДАЮ 50 ЭТО МАКСИМАЛЬНЫЕ МОИ УМОЛЯ 1.Высота BM параллелограмма АВCD делит стену АD на части 8 см и 14 см и ВМ=MD. АВCD найдите площадь параллелограмма.

2.Площадь параллелограмма 12 см2 и высоты ВК = 2см и ВМ =3 см. Найдите периметр параллелограмма.

3.Острый угол ромба QRMN делится на два отрезка высотой 600 и высотой QD длиной 6 см. Найдите площадь ромба.

1.

1) По условию ВМ=MD=14 см , где ВМ - высота параллелограмма АВCD.

2) AM+MD=AD

  8см + 14см = 22см - длина стороны AD.

3) S = AD · ВМ  - площадь параллелограмма АВCD.

22см · 14см = 308 см²

ответ: 308 см²

2.

Дано:

S = 12см²

ВК⊥AD

ВК = 2см

BM⊥DC

ВМ =3 см.

P=?

Решение.

1) S = AD · ВК  - площадь параллелограмма.

  AD = S : ВК

 AD = 12 : 2 = 6 см - одна сторона параллелограмма.

2) S = DC · ВM  - площадь параллелограмма.

  DC = S : ВM

 DC = 12 : 3 = 4 см - вторая сторона параллелограмма.

3) Р = 2· (AD+DС)  - периметр параллелограмма.

Р = 2 · (6 + 4) = 20 см

ответ: 20 см.

3.

Дано:

Ромб QRMN

∠QRM = 60°

QD⊥RM

RD = 6

S=?

Решение.

1) ΔQRD - прямоугольный треугольник.

∠RQD = 90°- 60° = 30°

2) Катет, лежащий против угла 30 градусов, равен половине гипотенузы.

RD =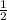 QR  =>   QR = 2RD

QR = 2 · 6 = 12см

QR=RM=MN=NQ  - как стороны ромба.

3) По теореме Пифагора  в прямоугольном треугольнике    

  RD²+DQ²=QR²    => DQ²=QR² - RD²

                                   DQ²=12² - 6²=144-36=108

                                    DQ = √108 = 6√3 см - высота ромба

4) S = RM · DQ - площадь ромба

 S = 12 · 6√3 = 72√3 ≈  125

ответ: 72√3 см²  или 125 см²