Даю 15. Найдите x+y, если (x;y)-решение системы уравнений:
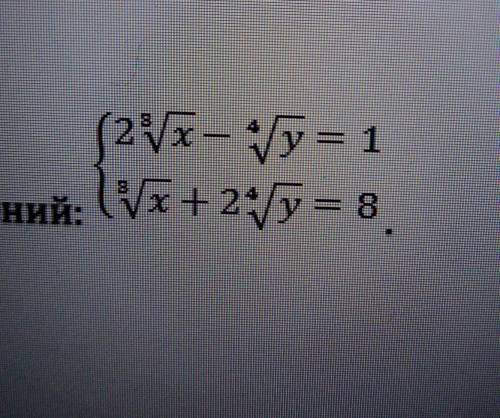
Другие вопросы по теме Алгебра
Популярные вопросы
- складіть розповідь про вірування давніх египтян. Поміркуйте які явища природи...
3 - 5 речень з фразеологізмами і синтактичний розбір...
3 -  Економічні зв‘язки Україна Франція...
3 - Задумане двоцифрове число що на 73 більше за добуток своїх чисел.Яке число?...
3 - Коп нуктенин орнына тыисты косымшаны койып окы...
3 - зробіть припущення, якт почуття могли викликати піраміди у давнього населения...
3 - Выпишите цитаты Какие Охарактеризуйте Ханського сина...
3 - на рисунке изображена схема электрической цепи,состоящей из источника постоянного...
1 - цікаві факти про бібліотеку Києво-Печерської лаври нужно ...
1 - Интервью - информационный публицистический жанр. (основы предложений)...
1
отнимаем от первого уравнения второе:
ОТВЕТ: x+y=256+81=337
Чтобы не таскаться пока со степенями, введём две замены:![v = \sqrt[8]{x}\ ,\ v \geq 0](/tpl/images/1574/7651/ac68f.png) ;
; ![u = \sqrt[4]{y}\ ,\ u \geq 0](/tpl/images/1574/7651/4b625.png) . Получаем систему:
. Получаем систему:
Воспользуемся методом сложения:
Тогда:
Обратная замена:
Тогда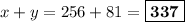 .
.
ответ: 337.