1. Алгебра
  2. дано пряму 2x - y + 4 =

дано пряму 2x - y + 4 = 0 і точку А(1;1). через точку А проведено пряму, паралельну даній, і пряму, перпендикулярну до данної. складіть рівняння цих прямих

aiau2004 aiau2004    3   10.08.2022 08:37    0

Ответы
aidar2002032 aidar2002032  10.08.2022 08:38

Параллельная прямая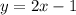 y = 2x - 1,  перпендикулярная прямая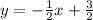 y = - \frac{1}{2}x + \frac{3}{2}

Объяснение:

Перепишем уравнение прямой в виде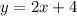 y = 2x + 4.

Тогда прямая, параллельная данной, имеет тот же угловой коэффициент, то есть записывается в виде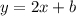 y = 2x + b.

Так как эта прямая проходит через точку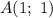 A(1;\,\,1), эти координаты должны удовлетворять этому уравнению:

1 = 2 \cdot 1 + b;b = - 1.

Значит искомое уравнение параллельной прямой: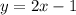 y = 2x - 1.

Угловые коэффициенты перпендикулярных прямых в произведении дают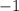 -1. Поэтому уравнение прямой, перпендикулярной данной, записывается в виде

y = - \displaystyle\frac{1}{2}x + b.

Так как и эта прямая проходит через точку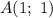 A(1;\,\,1), эти координаты должны удовлетворять этому уравнению:

1 = - \displaystyle\frac{1}{2} \cdot 1 + b;b = \displaystyle\frac{3}{2}.

Значит искомое уравнение перпендикулярной прямой:

y = - \displaystyle\frac{1}{2}x + \displaystyle\frac{3}{2}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
camcalol camcalol  18.05.2020 09:14
очень нужно! Вычислить десятый член арифметической прогрессии, первый член которой а1=8, а разность d=6...
daurmukhtar99 daurmukhtar99  18.05.2020 09:14
Решить уравнения. |b|=4 3(во второй степени)y-15=0 c - 16 =0 7х...
FantomLord24 FantomLord24  18.05.2020 09:14
При каких значениях x выражение 2+3x-88 равно 1)0;2)20;)3)-18;4)-70?...
ангелина67890 ангелина67890  18.05.2020 09:13
А) У выражение х+4/х-3 * 3х-9/х^2+8x+16 : 15/ху+4у b)Выполните действия: ((3/2х-1)/(3х-1/4х^2-1)-(6/3х-1)) * (3/2х-1) +((3х-1/3х-10)) -1...
грустнаякакахаха грустнаякакахаха  18.05.2020 09:13
Решите систему неравенств: * Подпись отсутствует (-∞;-9]∪[9;+∞) [-9;9] (-∞;+∞) ∅...
mery77 mery77  18.05.2020 09:13
заполнить таблицу по функции заданий формулой y=x(x-2)...
propprap propprap  18.05.2020 09:13
Решите систему уравнений сложения 3х - 8у = 14 3х + 5у = 1...
bogachea bogachea  18.05.2020 09:13
Какие из выражений являются целыми? А=3xy+ 0,5х²; B= а³: (а+1); C=3- 8 : х; D=7х² : 8...
198219821982 198219821982  05.08.2019 19:00
При яких значення a має зміст вираз? a+3/a-7...
саша4265 саша4265  05.08.2019 19:00
Купили 16тетрадкй по 22 копейки и по 45к ,заплатив за всю покупку 4р67к.сколько купили тетрадей каждого вида...

Популярные вопросы