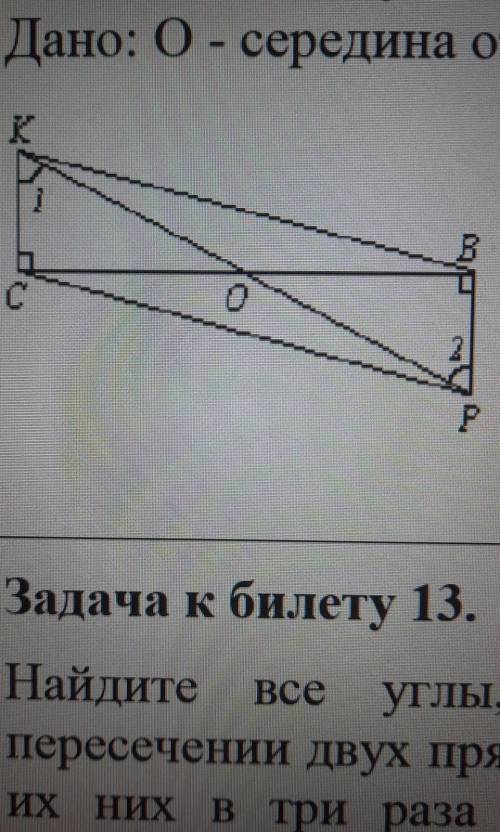
Дано: О - середина отрезка BC, KC⊥СO и PB⊥BO (см. рис.). Докажите: а) ∠1 = ∠2. б) ВК = CP
Другие вопросы по теме Алгебра
Популярные вопросы
- Действующие вулканы мира список названий...
2 - Сочинение по биологии на тему жизнь растений зимой...
2 - Християнська церква вчила, що господь поділив усіх людей на три верстви. укажіть...
3 - Яке правопорушення не відноситься до проступків...
2 - Укрокодила на передних лапах по пять пальцев на задних по 4 сколько всего...
1 - Вкорне 5 - 4x = 3,2 решить уравнение...
1 - Музыкальная группа ласковый май дадут концерт в зале, вмещающем 2 120 зрители.цена...
2 - Напишіть рівняння реакцій які дозволяють здійснити такі перетворення zn-zno-znso4...
3 - 1) косы у 2) сосуд 3)(не) слова 4)(не) тайна 5)(не) настная погода 6) травы...
2 - Вкаких эпизодах показано пондевольное положение герасима и других дворовых...
3
Объяснение:
1) КС⊥ СО, т.е. КС ⊥СВ
ВР ⊥ВО, т.е. ВР ⊥СВ
По признаку параллельности прямых, если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны». Следовательно, КС ║ВР
2) ∠1 и ∠2 - это накрест лежащие углы, т.к. КС ║ВР, то и
∠1 = ∠2.
3) ΔСКВ и ΔСРВ - прямоугольные. ∠1 = ∠2. СВ - общая сторона (катет)
ΔСКВ = ΔСРВ по катету и противолежащему острому углу. Следовательно,
КВ = СР, ч.т.д.