Дано квадратное уравнение 2x^2-8x+c=0 найдите корни (с решением)
Другие вопросы по теме Алгебра
Популярные вопросы
- , нужно ответить про Казахстан на все вопросы...
1 - 5. Мәтінді оқып, құрмалас сөйлемдерді түріне қарай ажыратып жаз. Біріккен...
2 - Знайдіть у тексті Мытькокозавр з Юрківки, або Химера лісового лісу...
3 - Алгебра 8 класс: решите уравнение (x-3)^4-625=0...
2 - Составить диалог на тему мы в деревне...
1 - Чим було зумовлено стримування реформаторської діяльності останнього...
3 - Подготовьте сообщение об Соне Делоне ,которая внесла вклад в развитие...
3 - В 1. На контурной карте с карты в учебните обозначь красным кружком...
2 - Кикиморские сказки Русинова выписать цитату и рисунок к этой цитате...
3 - Відмінні риси між Журденом і Дорантом ...
2
Объяснение: 2x²-8x+c = 0.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант: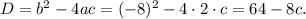
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: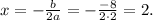 Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: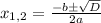 . Выразим каждый из корней:
. Выразим каждый из корней:
Аналогично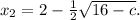
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня: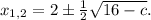
ОТВЕТ: если с < 8, то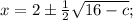 если с = 8, то х = 2; если с > 8, то корней нет.
если с = 8, то х = 2; если с > 8, то корней нет.