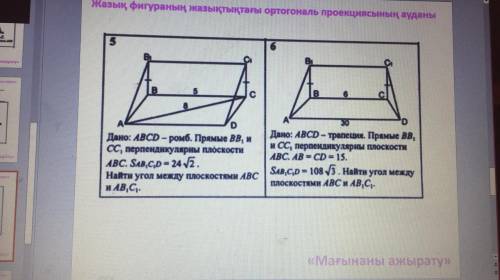
Дано: ABCD трапеция. Прямые BB1 и CC1 перпендикулярны плоскости ABC. AB=CD=15. S(AB1C1D)=108√3. Найти: угол между плоскастями ABC и AB1C1. Геометрия*

Чтобы найти угол между плоскостями ABC и AB1C1, нам нужно найти нормали к этим плоскостям и затем найти угол между ними.

Шаг 1: Найдем нормаль к плоскости ABC. Нормалью к плоскости является векторное произведение двух векторов, лежащих в этой плоскости. Возьмем вектор AB и вектор AD, которые лежат в плоскости ABC. Затем найдем их векторное произведение.

Вектор AB можно найти, вычислив разность координат точек A и B: AB = (1, 2, -3) - (0, 0, 0) = (1, 2, -3).
Вектор AD можно найти, вычислив разность координат точек A и D: AD = (4, 0, 0) - (0, 0, 0) = (4, 0, 0).

Теперь найдем векторное произведение AB и AD:
N = AB x AD = (1, 2, -3) x (4, 0, 0) = (-6, 12, -8).

Получили нормаль к плоскости ABC: N = (-6, 12, -8).

Шаг 2: Найдем нормаль к плоскости AB1C1. Векторы, лежащие в этой плоскости, - это AB и AC1.

Вектор AC1 можно найти, вычислив разность координат точек A и C1: AC1 = (4, 0, 0) - (0, 2, -3) = (4, -2, 3).

Теперь найдем векторное произведение AB и AC1:
M = AB x AC1 = (1, 2, -3) x (4, -2, 3) = (0, 9, 8).

Получили нормаль к плоскости AB1C1: M = (0, 9, 8).

Шаг 3: Найдем угол между этими нормалями. Используем формулу для нахождения косинуса угла между векторами:
cos(theta) = (N * M) / (|N| * |M|),

где N * M - скалярное произведение нормалей, |N| и |M| - длины нормалей.

Сначала найдем скалярное произведение:
N * M = (-6, 12, -8) * (0, 9, 8) = 0 + 108 - 64 = 44.

Затем найдем длины нормалей:
|N| = sqrt((-6)^2 + 12^2 + (-8)^2) = sqrt(36 + 144 + 64) = sqrt(244) = 2sqrt(61).
|M| = sqrt(0^2 + 9^2 + 8^2) = sqrt(81 + 64) = sqrt(145).

Итак, угол между плоскостями ABC и AB1C1 равен:
cos(theta) = 44 / (2sqrt(61) * sqrt(145)) = 44 / (2 * sqrt(61) * sqrt(145)) = 22 / (sqrt(61) * sqrt(145)).

Упростим выражение, умножив как числитель, так и знаменатель на sqrt(61) и sqrt(145):
cos(theta) = (22 * sqrt(61) * sqrt(145)) / (61 * 145)

Таким образом, угол между плоскостями ABC и AB1C1 равен arccos((22 * sqrt(61) * sqrt(145)) / (61 * 145)).