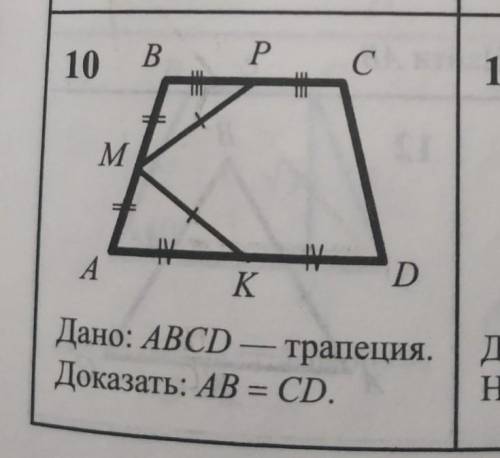
Дано ABCD-трапеция Доказать AB=CD

Для доказательства того, что AB=CD в данной ABCD-трапеции, воспользуемся свойствами трапеции.

Для начала, давайте определим свойства трапеции. Трапеция - это четырехугольник, у которого одна пара противоположных сторон параллельна. В данной трапеции стороны AB и CD являются параллельными сторонами.

Теперь, чтобы доказать, что AB=CD, мы можем использовать два способа: построение параллельных линий или равенство углов.

1. Построение параллельных линий:

Пусть E и F - точки пересечения диагоналей AC и BD со стороной AB, соответственно. Также пусть G и H - точки пересечения диагоналей AC и BD со стороной CD, соответственно.

Так как AB || CD (по свойствам трапеции), то имеем следующие параллельные отрезки: AE || CF и BE || DF.

С помощью этих параллельных отрезков, можем применить теорему трикотажа, согласно которой:

AE/CF = AB/CD (маленькая трапеция AEBF подобна маленькой трапеции CFHD)

BE/DF = AB/CD (маленькая трапеция BDEF подобна маленькой трапеции FDHG)

Из этих двух уравнений мы можем заключить, что AE/CF = BE/DF.

Теперь воспользуемся теоремой Хэйла, согласно которой:

AE/BE = CF/DF

Так как AE/CF = BE/DF и AE/BE = CF/DF, то мы получаем, что AE/BE = AE/BE. Это значит, что отрезки AE и BE равны.

То есть, AB = AE + EB = BE + AE = BE + EB = CD.

Таким образом, мы доказали, что AB = CD в данной ABCD-трапеции.

2. Равенство углов:

Другой способ доказательства AB = CD в данной ABCD-трапеции - это использование равенства углов.

Заметим, что угол ABC и угол CDA являются вертикальными углами (углами, образованными пересекающимися прямыми линиями), и, следовательно, они равны.

Также, угол BAC и угол DCA являются одними и теми же углами (углы при основаниях равнобедренной трапеции), и, следовательно, они равны.

Поскольку угол ABC = угол CDA и угол BAC = угол DCA, то угол ABC + угол BAC = угол CDA + угол DCA.

Это означает, что сумма углов ABC и BAC равна сумме углов CDA и DCA.

Так как сумма углов в треугольнике равна 180 градусам, то мы можем записать следующее уравнение:

180 градусов = угол ABC + угол BAC = угол CDA + угол DCA.

Заметим, что угол ABC + угол BAC = угол CDA + угол DCA.

Таким образом, приравняв эти две суммы, мы получим:

угол ABC + угол BAC = угол CDA + угол DCA.

Используя свойство равенства углов, мы можем записать следующее равенство:

угол ABC = угол CDA.

Теперь, заметим, что у угла ABC и угла CDA идентичные стороны AB и CD.

Следовательно, мы можем заключить, что AB = CD.

Таким образом, мы также доказали, что AB = CD в данной ABCD-трапеции.

В итоге, мы смогли доказать равенство сторон AB и CD в данной ABCD-трапеции, используя два разных метода: построение параллельных линий и равенство углов.