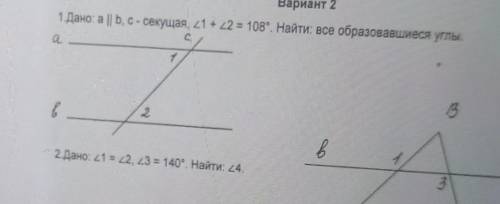
Дано: а||b, c - секущая. Угол 1 +угол 2 =108°. Найти все образовавшиеся углы

∠1=54°;∠2=54°

Объяснение:

Несложно заметить, что ∠1=∠2, т.к. они накрест лежащие, поэтому можем составить уравнение

2*∠1=108°

∠1=54°

Дано, что а||b, c - секущая и угол 1 + угол 2 = 108°.

Для решения этой задачи, нам необходимо использовать две основных свойства параллельных линий и секущих.

Первое свойство: Когда прямые секущая и параллельная к ней пересекают две параллельные линии, образуется система соответствующих, внутренних и внешних углов.

В данном случае угол 1 и угол 2 являются соответствующими углами, так как они находятся с одной стороны линий а и b и пересекают секущую линию c.

Второе свойство: Парные соответствующие углы равны между собой.

Теперь, используя эти свойства, мы можем найти все образовавшиеся углы.

Угол 1 и угол 2 являются парными соответствующими углами, поэтому они равны между собой. Исходя из этого, мы можем записать следующее уравнение:

Угол 1 = Угол 2

Из условия задачи, мы также знаем, что сумма угла 1 и угла 2 равна 108°:

Угол 1 + Угол 2 = 108°

Подставим значение угла 1 в это уравнение:

Угол 1 + Угол 1 = 108°

2 * Угол 1 = 108°

Теперь найдем значение угла 1:

Угол 1 = 108° / 2

Угол 1 = 54°

Так как угол 1 и угол 2 равны между собой, то угол 2 также будет равен 54°:

Угол 2 = 54°

Таким образом, образовавшиеся углы в данной задаче составляют:

Угол 1 = 54°
Угол 2 = 54°

Ответ: Угол 1 равен 54°, угол 2 равен 54°.