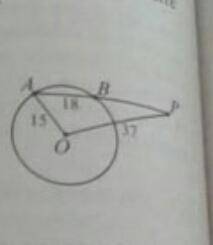
Дана окружность с центром в точке O радиуса 15 и точка P такая, что OP=37.через точку P проведена прямая,пересекающая окружность в точках A и B таких,что AB=18.найдите длину отрезка BP.

ответ: 25

Объяснение: Тут Надо делать получается 18-15=3 и 37-15=22 И мы потом Всё это складываем

Для решения данной задачи, нам понадобится использовать свойства окружностей и прямоугольных треугольников.

Итак, у нас дана окружность с центром в точке O и радиусом 15. Точка P находится на расстоянии 37 от центра окружности O. Значит, OP = 37.

Нам также известно, что прямая, проведенная через точку P, пересекает окружность в точках A и B. И длина отрезка AB равна 18.

Обозначим точку пересечения прямой и окружности как точку M.

Согласно свойству окружностей, радиус, проведенный к точке пересечения прямой и окружности, будет перпендикулярен к этой прямой. Из этого следует, что PM перпендикулярна к AB.

Давайте рассмотрим треугольник OPM. Мы знаем, что OP равно 37, а радиус окружности O равен 15. Поэтому можем использовать теорему Пифагора для нахождения длины PM.

PM^2 = OP^2 - OM^2
PM^2 = 37^2 - 15^2
PM^2 = 1369 - 225
PM^2 = 1144
PM = √1144
PM ≈ 33.82

Затем, обратим внимание на треугольник PAB. У нас есть сторона AB, которая равна 18, и мы хотим найти длину отрезка BP. При этом, мы уже знаем значение PM, которое равно примерно 33.82.

Чтобы найти BP, мы можем использовать следующую формулу для нахождения длины отрезка в прямоугольном треугольнике:

BP^2 = AB^2 - PM^2
BP^2 = 18^2 - 33.82^2
BP^2 = 324 - 1144
BP^2 = -820

Однако, получаем отрицательное значение при вычислении. Это означает, что треугольник PAB не является прямоугольным, а следовательно, у нас нет достаточно информации для вычисления длины отрезка BP.

Таким образом, мы не можем найти длину отрезка BP с использованием только данных из задачи.