Дана функция y=x³-x²+4. Найдите: а) промежутки возрастания и убывания функции
б) точки экстремума
в) наибольшее и наименьшее значения функции на отрезке [1;4]
Другие вопросы по теме Алгебра
Популярные вопросы
- Известно, что вероятность рождения близнецов одного пола - 0.64. рассмотрели...
3 - Расстояние в 45 км по озеру моторная лодка преодолевает за 5 часов. точно...
3 - Участку цепи с сопротивлением 12 ом приложено напряжение 12в какое количество...
2 - Почему права ребенка отличаются от прав взрослого человека?...
1 - 4x(x-3x+2)=. представить в виде многочлена (2-4)...
3 - 1)чему равно атмосферное давление на уровне моря на широте 45 при температуре...
3 - Сократите дроби 1)15\100. 2)59\100. 3)35\100. 4)85\100...
3 - Бригада из пяти плотников и одного столяра выполнила работу. бригада из...
2 - Що таке прикметник на які питання відповідає...
3 - Сад в форме квадрата окружён забором, одна сторона катор ого равна 121...
1
a) Возрастает: (-∞;0)∪(2/3;∞), убывает: (0;2/3)
б) 0 - локальный максимум, 2/3 - минимум
в) Наибольшее y=52 при x=4, наименьшее: y=4 при x=1
Объяснение:
Производная равна: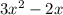 . Отсюда x1=0, x2=2/3. Это точки экстремума.
. Отсюда x1=0, x2=2/3. Это точки экстремума.
б)
0 - максимум
2/3 - минимум
а)
На основании максимума и минимума получаем:
Функция возрастает (-∞;0)∪(2/3;∞)
Функция убывает (0;2/3)
в)
На всем промежутке от 1 до 4 функция возрастает, поэтому наименьшее значение y=4 находится при x=1, а наибольшее y=52 находится при x=4.
Нужно просто подставить 1 и 4 в функцию вместо x, чтобы вычислить y.