1. Алгебра
  2. Дана функция y=f(x), где

Дана функция y=f(x), где f(x)=tgx. Верно ли, что значение выражения f(3x+10π)+f(7π−3x)=1?
(Желательно с объяснением)

СыроКок1 СыроКок1    3   08.12.2020 14:16    1

Ответы
iIИльяIi iIИльяIi  07.01.2021 14:17

f(x)=\mathrm{tg}x

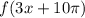Найдем f(3x+10\pi):

f(3x+10\pi)=\mathrm{tg}(3x+10\pi)

Так как основной период тангенса равен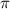 \pi, то выражение можно упростить:

\boxed{f(3x+10\pi)=\mathrm{tg}3x}

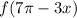Найдем f(7\pi-3x):

f(7\pi-3x)=\mathrm{tg}(7\pi-3x)

Опять же учитывая периодичность тангенса, получим:

f(7\pi-3x)=\mathrm{tg}(-3x)

Зная, что тангенс - нечетная функция, получим:

\boxed{f(7\pi-3x)=-\mathrm{tg}3x}

Получим:

f(3x+10\pi)+f(7\pi-3x)=\mathrm{tg}3x-\mathrm{tg}3x=0

Таким образом, выражение равно 0, а не 1.

ответ: нет, неверно

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Keks5478568 Keks5478568  18.09.2019 00:30
Как найти одз в примерах: 2x(x-10) 3(x-20)(x+20)...
bon1101 bon1101  18.09.2019 00:30
Уравнение x^3-4x=0 в ответ запишите меньший корень...
ира09н9 ира09н9  18.09.2019 00:30
Решите уравнение x^4+2x^2=0 в ответ запишите сумму корней или корень если он один...
Neznayka56000 Neznayka56000  18.09.2019 00:30
Представьте в виде многочлен (0,2х+0,5у)^3...
УмничкаKris УмничкаKris  18.09.2019 00:30
Преобразовать выражение в многочлен стандартного вида (3+x)(x--x)^2 (2x-4)^2-(2x+3)^2...
Mv0856 Mv0856  18.09.2019 00:30
Составьте краткое уравнение, если его корни 3 и 5...
kaba4ok2001 kaba4ok2001  18.09.2019 00:30
Представьте выражение в виде многочлена (1/2а-1/3b^2)^3...
Løæålø Løæålø  18.09.2019 00:30
Выражение: дробь 15b разделить на 3-b+ дробь 8b разделить на b^2-9 умножить на дробь 7b+21 делённое на 4...
kmtva04 kmtva04  18.09.2019 00:30
Решить уравнение 4(3 - 2 х) - 11= 7...
машина34 машина34  18.09.2019 00:30
Представьте выражение в виде многочлена (1,5m^3+0,3m^4)^3...

Популярные вопросы