Дана функция y=f(x), где f(x)=12^x. Вычислить: f(sin^2 x)⋅f(cos^2 x).
с объяснением.
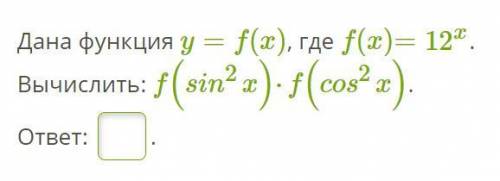
Другие вопросы по теме Алгебра
Популярные вопросы
- Разряды прилагательных - большой , библиотечный , арлиный ,бездарный...
3 - Тест «класс млекопитающие» а1. млекопитающие населяют сушу, моря, пресноводные...
2 - Почему кремниевая кислота вытесняется из её солей угольной кислотой при...
1 - Суравнением семь девятых икс плюс одиннадцать двенадцатых (обычные дроби)ответ...
3 - Как характеризует андрея соколова его отношение у письмам с фронта...
1 - Сколько раз выполняется оператор цикла с параметром...
3 - Расстояние между a и b равно 730 км . из города a в город b выехал первый...
2 - Катер шёл по течению реки. скорость катера a км/ч, скорость течения v...
3 - Cos2x-0,5sin2x=1 найдите самый отрицательный корень уравнения...
1 - Электроплитка включега в сеть с напряжением 220 вт и силой тока 5 ам.сколько...
3
При решении было применено основное тригонометрическое
тождество : Sin²α + Cos²α = 1