Дана функция : 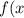 = (4x + 1) \sqrt{x - 1} ) найти: f'(5)варианты ответа: а)8 1/3. в)13 1/4. с)12. д)4. е)1 3/4. с решением ,
найти: f'(5)варианты ответа: а)8 1/3. в)13 1/4. с)12. д)4. е)1 3/4. с решением ,
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите х и у чень нужна ваша...
1 - Номер 426 учебник пименова 7 класс подчеркнуть однородные члены предложеня...
2 - Рассмотрите иллюстрацию И. Л. Бруни на форзаце 1. Найдите строки из текста...
2 - Что осуждает Алеша? К чему тянется? Детство М. Горький...
1 - Найдите значения выражения...
1 - Решите уравнение 3х/х+5 +1=10/х2+10х+25...
3 - 14/25-4/5:2/3 подробно 1/2+5/6:(1целая 1/2-3/4)*1 целую...
3 - Решите номера по математике...
3 - Размышлениями о том, насколько мучителен бывает путь к самому себе, цели...
3 - Описание фото По 5 пунктам описать надо....
1
ответ:13 1/4.
Объяснение: