Дана функция. необходимо исследовать её на возрастание(убывание) и экстремумы.
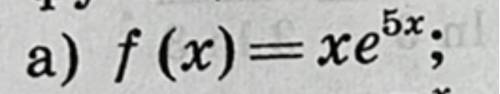
Другие вопросы по теме Алгебра
Популярные вопросы
- Система состоящая из невесомых блоков, невесомых и нерастяжимых...
2 - Човні на глибині 5 м утворилась пробоїна площею 0,2 м2. З якою...
2 - 1-тапсырма. Оқылым. Берілген өлеңдерді оқып, тапсырмаларды орындаңыз.1-өлеңАқкиімді,...
3 - На поверхность жидкости падает луч под углом 450. Угол преломления...
3 - Что будет если списал диктант в 4 классе оставят на 2 год?...
3 - 1-тапсырма Тәуелдеу (Отан, мектеп) сөздерін 2-тапсырма Фонетикалық...
3 - Эссе зима и лето в маем городе 120 140 слов...
3 - с английским,там очень легко,это видно,но не для меня)Номер 6....
3 - Написать по 2 предложения Passive Voice 1. Past 2.Present 3.Future...
1 - 14. Мәтінді көркем жаз. . 1 мамыр - Қазақстан халқының бірлігі...
3
Функция
- убывает на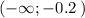
- возрастает на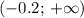
Точка минимума функции:
x = -0.2
Объяснение:
Функция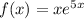 определена на R, или
определена на R, или 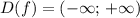
Для нахождения промежутков возрастания (убывание) и точек экстремума находим производную функции f'(x):
Производная исследуемой функции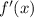 также определена на R, или
также определена на R, или 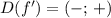
Найдем критические точки
Т.к. производная исследуемой функции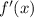 также определена на R, или
также определена на R, или 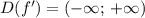 , найдем нули производной :
, найдем нули производной :
что равносильно совокупности:
Найдем промежутки возрастания / убывания:
Функция возрастает при f'(x) > 0
убывает при f'(x) < 0
Для этого исследуем точку x = -0,2 на экстремум: знак производной
- при х < -0.2 f'(x) < 0 => функция f(x)
убывает на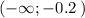
- при х > -0.2 f'(x) < 0 => функция f(x)
возрастает на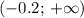
В точке x = -0.2 происходит смена функции
с убывания --> на возрастание
Следовательно, x = -0.2 - является единственной точкой экстремума, а именно это - точка минимума функции