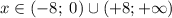Дана функция f(x) где f(x)=x в -3 степени. найдите все значения х при которых выполняется неравенство х в квадрате/f(x)> 64*f(1/x)
Другие вопросы по теме Алгебра
Популярные вопросы
- Мне. напишите эксперементы для детей 11-13 лет....
2 - Найдите сущ. 2-ого скл. озеро поле рожь подъезд...
3 - Какой объект был назван именем с.дежнёва? !...
3 - Отношение разности двух соседних оцифрованных значений шкалы измерительного...
3 - Объясни,как ты понимаешь выражения. влачить жалкое существование-...
1 - Какя гора является высочайшей точкой земли...
2 - Сумма двух углов равна 180°. являются ли эти углы смежными. если...
1 - Рогатый баран скрещен с тремя овцами. • от первой овцы родились...
1 - 4.щелочные металлы проявляют сильные: а) окислительные свойства;...
1 - Запишите краткое лексическое значение слова-романтика....
1
Требуется решить неравенство
для функции, заданной как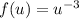 .
.
В таком случае имеем
Упрощаем неравенство
Имеем интервалы знакопостоянства:
ответ: при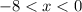 и
и 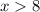 .
.
Условная запись ответа объединением множеств: