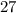Дана арифметическая прогрессия
…23; х; 31….
Найди х
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить вычитание смешанных дробей 3 целых 12/70 - 2 целых 3/5...
2 - Напиши строчку слова some и каждого из двух словосочетаний...
2 - Мама налепила 200 пельменей, она разложила их по пакетам. в 4 маленьких пакетах...
1 - Для хранение керосина массой 8 кг необходим сосуд емкостью не менее...
1 - Асо словами языковой и человечное кто знает предложения?...
2 - Визнач валентність атомів елементів : а) у сполуках шз хлором,знаючи,що він...
2 - Начертить один отрезок 7 см! а другой на 4 см короче. найди сумму этих отрезков....
2 - 1) (-3a-2b)² 2) (4a+2b)³ 3) (a²+2x)³ 4) (8y-4x)² плз: 33...
2 - Характеристика жилина и костылина из рассказа кавказский пленник(толстой) кратко...
1 - Статья по онглийски как она читается по руски the countri and the city...
2
aₙ = a₁ + (n-1) * d,
где aₙ - общий член прогрессии до n-го члена,
a₁ - первый член прогрессии,
n - номер члена прогрессии,
d - разность между соседними членами прогрессии.
В данном случае у нас даны два члена прогрессии: 23 и 31. Мы должны найти х — третий член прогрессии.
Известно, что разность между соседними членами прогрессии постоянна. Чтобы найти эту разность, можем вычислить разность между вторым и первым членами:
d = 31 - 23 = 8.
Теперь, зная разность d, можем найти х — третий член прогрессии с помощью формулы общего члена:
a₃ = 23 + (3-1) * 8 = 23 + 2 * 8 = 23 + 16 = 39.
Таким образом, третий член прогрессии равен 39.
Ответ: х = 39.
ответ: