Дана арифметическая прогрессия -15, -12, . а) определите её разность б) запишите формулу n-го члена этой прогрессии в) выясните, содержится ли в этой прогрессии число 12 и если да, то пол каким номером г) определите, сколько в этой прогрессии положительных членов !
Другие вопросы по теме Алгебра
Популярные вопросы
- Пещерный храм аджанты архитектурные элементы(колонны и т.д)...
2 - Тіло рухається з точки а(5; 8) до точки в(-6; 4) а потім до точки c(-1;...
1 - Выберите их списка неисчисляемые существительные: room,boot,cheese,orange,cake,sweet,honey,salt,boy,friend,match,brush,window,...
3 - Рассказ что вы бы делали с волшебной па...
2 - Как выделить члены предложения графически ?...
3 - 4речення з простим і складеним присудком...
1 - 3. вставьте, где нужно, непроизносимую согласную букву, напишите проверочное...
1 - 5circle the correct item. 1) is there some/any milk in the tidget? 2)there...
1 - Цена груш — x р. за 1 кг, а цена яблок — y р. за 1 кг. запиши в виде выражения:...
2 - Вырази в более мелких единицах длины. 1дм 3см=? см. 3дм 7см=? см. 9дм 5см=?...
1
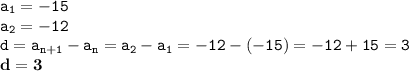
б)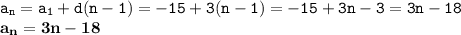
в)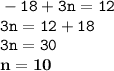
г)получается, что количество положительных членов бесконечно
ответ: а)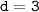 ; б)
; б) 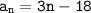 ; в)
; в)  ; г) бесконечное множество
; г) бесконечное множество
Дана арифметическая прогрессия -15, -12, ..., то есть a₁= -15, a₂= -12. Тогда
а) её разность:
d = a₂ - a₁ = -12 - (-15) = -12 + 15 = 3.
б) формула n-члена этой прогрессии :
a(n) = -15+3·(n-1)
в) выясним, содержится ли в этой прогрессии число 12:
a(n) = 12 или
-15+3·(n-1) = 12
3·(n-1) = 12 + 15
3·(n-1) = 27
n-1 = 27:3
n = 9+1=10∈N
Содержится под номером 10.
г) Так как d=3 >0, то в этой прогрессии бесконечное количество положительных членов. В самом деле:
a(n) = -15+3·(n-1)>0
3·(n-1)>15
n-1>15:3
n>5+1
n>6
Начиная с 7-члена арифметической прогрессии все члены положительные. Так как множество натуральных чисел N бесконечно, то положительных членов арифметической прогрессии бесконечно.