Дана арифметическая прогрессия: 33; 25; 17; … . найдите первый отрицательный член этой прогрессии. те кто не равнодушен мне !
Другие вопросы по теме Алгебра
Популярные вопросы
- В 336 году до н.э. царем Македонии стал 20-летний Александр, получивший прозвище...
2 - Ознакомьтесь с данными высказываниями. Какую информацию о писа- теле вы получили?...
2 - Напишите эссе «А. Байтурсынов, его роль в истории казахского общества...
3 - Эссе повествование на тему почему мы должны беречь леса ПОМАГИТЕ...
2 - Алгебра 2)4-t)^33)(a^3-0,2b)^34)(0,2x^5-5y^4)^35)(1/2a^6-4b^3)^3 подпишусь...
3 - За грибами Осе(нн/н)им утром мы (за/зо)гл..нули (в)лес пр..б..жал в..т..рок...
2 - Греко-македонское войско встретило ожесточенное сопротивление народов Центральной...
3 - Choose the correct answer A, B or C...
3 - R1=6 ОмR2=4 ОмА=9 АА2= 3 Анайти:R3-?хэлпаните...
2 - Визнач норипльний атмосферний тиск для своєї місцевості...
3
Дана арифметическая прогрессия: 33; 25; 17; …
а₁=33
d=a₂-a₁=25-33=-8
аₙ<0
По формуле аₙ=а₁+d(n-1), значит т.к. аₙ<0, то
а₁+d(n-1)<0
33-8(n-1)<0
33-8n+8<0
41-8n<0
-8n<-41
n>41/8
n>5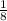 , т.е. минимально возможное n=6(т.к. это должно быть целое число)
, т.е. минимально возможное n=6(т.к. это должно быть целое число)
Подставляем аₙ=а₁+d(n-1)=33-8(6-1)=33-8*5=33-40=-7