Дан эллипс: F 1,2 =(+-5;0) и B 1,2=(0;+-2). Напишите уравнение эллипса, найти оси и эксцентриситет

ответ: Уравнение эллипса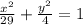 ; оси симметрии данного эллипса являются осями координат(или ось Ох и Оу); ε =5/√(29)

Объяснение:

Дан эллипс: F₁ =(-5;0); F₂ =(5;0)  и B₁=(0;-2); B₂=(0;2). Напишите уравнение эллипса, найти оси и эксцентриситет

фокусное расстояние эллипса с = 5 (от точки F до точки О)

малая полуось b = 2

большая полуось а находится из соотношения

                             а² = b² + c²

                             a² = 2² + 5² = 4 + 25 = 29

уравнение эллипса:

- каноническое уравнение эллипса

Оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии.

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом .

ε = с/ a = 5/√(29)