дам 20б.
Решить уравнение используя снижения порядка
x(y''+1)+y'=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте рассказ о начале Великой французской революции от имени аристократа или...
3 - Почему реформы Тюрго потерпели неудачу?...
3 - В чём причины Семилетней войны и каковы её итоги?...
1 - Назовите характерные черты века Просвещения?...
2 - Какие идеи высказывал Вольтер? Нет ли, на ваш взгляд, в них противоречивости? Свою...
3 - Представьте себя «патриотом» или «лоя-листом». Какие аргументы вы приведёте в защиту...
3 - Можно ли говорить, что идеи Ж.-Ж. Руссо были наиболее радикальными по сравнению...
3 - Какими чертами характеризовался стиль рококо?...
1 - Какими «естественными правами», по мнению просветителей, должны быть наделены люди?...
1 - В чём заключается значение идей Ш.-Л. Монтескье о разделении властей?...
2
Понизим порядок с замены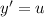 , тогда
, тогда 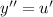
Выполним обратную замену