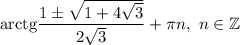Ctgx-√3tgx+1=0
решите уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- твір на тему: Life in future 20 речень на англійській ...
2 - Подумайте, почему Религиозному образованию мусульман страны уделяется...
3 - Визначте коло проблем порушених в оповіданні поясніть одну з них А.Азімов...
3 - Перетвори звичайний дріб у десятковий ...
1 - по образцу из книги септігі неге жалғанған ? Үлгі : Кітап әпер . Мына...
1 - Як гетьмани та козацька старшина відстоювали суверинітет Козацької держави?...
1 - по образцу в книге .1. Марат қызын мектептен әкеле жатыр . ( Ұл ) . 2....
1 - Казак адебиети комек тесип жибересиздер ме...
3 - Синтаксичний розбір речень та підчеркнуть члени речення....
2 - Основою економіки ціеї країни-архіпелагу є туризм і банківські послуги;...
2
ОДЗ: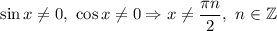
Домножим на тангенс, который не может равняться нулю:
ответ: