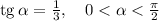Cos(arctg(1/3)+arcctg(-корень из 3))
Другие вопросы по теме Алгебра
Популярные вопросы
- Ilike to skate and bike.my mum likes to read books.my father drive...
1 - Какая масса меди может быть вытеснена из соли металлом, массой 1г,...
3 - Описать симбиоз между нильский крокодил - сенегальская авдотка...
2 - Мен кумырска болсам , эссе жазу керек комектесиндерши...
3 - Оқушы күнделікке не жазады? мұғалім күнделікке не қояды? күнделікті...
1 - Реши . в магазин 200кг лимонов и мандарин 5 ящ лимонов по 20кг в...
3 - Нужен рассказ(10-15 предложений) на тему мой любимый певец/любимая...
3 - Сравни произведения 32×2и 36×2 сравни записи, какая между ними разница,...
3 - Какие из следующих утверждений верны? 1. существует квадрат, который...
2 - Выписать из комедии ревизор предложения с однородными сказуемыми...
1
Пусть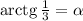 , тогда
, тогда