Алгебра: Cos(2x-п/2)=√2/2 тригономическое уравнение решить

Cos(2x-п/2)=√2/2 тригономическое уравнение решить

Ответы

lerafrank26022 19.11.2020 01:04

$cos\Big(2x-\dfrac{\pi}{2}\Big)=\dfrac{\sqrt2}{2}\\\\\\2x-\dfrac{\pi}{2}=\pm \dfrac{\pi}{4}+2\pi n\ ,\ n\in Z\\\\\\2x=\pm \dfrac{\pi}{4}+\dfrac{\pi}{2}+2\pi n\ ,\ n\in Z\\\\\\x=\pm \dfrac{\pi}{8}+\dfrac{\pi}{4}+\pi n\ ,\ n\in Z\\\\x=\left[\begin{array}{l}\ \, \dfrac{\pi}{8}+\pi n\ ,\ n\in Z \\ \dfrac{3\pi}{8}+\pi n\ ,\ n\in Z\end{array}\right\frac{x}{y}$

ПОКАЗАТЬ ОТВЕТЫ

Daniil3037 19.11.2020 01:04

Уравнение

$cos(2x-\dfrac{\pi}{2}) = \dfrac{\sqrt2}{2}$

Для начала сделаем преобразование левой части уравнения: используем переместительный закон, чтобы изменить порядок членов, затем вынесем знак минуса за скобки, избавимся от минуса за счет свойств честности или нечетности тригонометрических функций, и, наконец используем выражение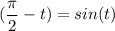 $(\dfrac{\pi}{2} - t) = sin (t)$ для преобразования.

$cos(2x-\dfrac{\pi}{2}) = cos(-\dfrac{\pi}{2}+2x) = cos(-(\dfrac{\pi}{2}-2x)) = cos(\dfrac{\pi}{2}-2x) = sin(x)$

После преобразования решаем далее

$sin(x) = \dfrac{\sqrt2}{2}$

Уравнение имеется два решения

$sin(x) = \dfrac{\sqrt2}{2} \\\\ \boxed { arcsin(\dfrac{\sqrt2}{2})= \dfrac{\pi}{4}}\\\\2x = arcsin(\dfrac{\sqrt2}{2})\\\\2x = \dfrac{\pi}{4}\\\\2x = \dfrac{\pi}{4} + 2\pi n, ~~n \in Z\\x = \dfrac{\pi}{8}, ~~n \in Z \\\\\\cos(\pi - 2x) =arcsin(\dfrac{\sqrt2}{2})\\\\\pi-2x= \dfrac{\pi}{4}\\\\\pi -2x=\dfrac{\pi}{4}+2\pi n,~~n \in Z\\\x = \dfrac{3\pi}{8}-\pi n,~~n \in Z$