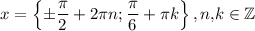Cos^2-√3sinxcosx=0 как решить это уравнение?
Другие вопросы по теме Алгебра
Популярные вопросы
- 4Order the words to make sentences andquestions with was and were....
3 - Кто такой митрополит Алексей...
1 - короткий текст по названию где я живу на английском.Желательно напишите про...
3 - ? 1. Почему после столетией войны королям обеих стран пришлось опять, ироться...
2 - Выполните дам лучший кто первый ответит...
1 - 1.Гасн…т багря…ый луч со…нца. 2.Морозные туман…ые сумерки опускают…ся над...
3 - Найдите площадь закрашенной фигуры рисунок 11...
1 - Тіло масою 2 кг набуває Швидкість 8 м/с, взаємодіючи з іншим тілом, якеотримує...
1 - Определите давление, которое оказывает на арену цирковой слон, стоящий на...
2 - Как улететь в космос, как Кайто?...
1
Условие: cos²x - √3sin(x)·cosx = 0
Разобьём правую часть на множители. Приравняем каждый множитель к нулю и решим простые тригонометрические уравнения.
cos(x)(cosx-√3sinx) = 0
Если sinx=0, то cosx = √3·0 = 0, но синус и косинус одного угла не могут одновременно равняться нулю. Поэтому делить на sinx можно.
ответ: