Числовая окружность. Кто может пояснить почему мы берём именно 3 углов прямых и добавляем их к сумме , и как их найти?, если считать без калькулятора возможно их найти самому, объясните как?.

Так как при вращении на 360°=2П радиан , мы попадаем в ту же точку ,

то угол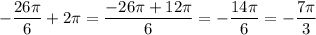        попадает в ту же

точку на единичной окружности , что и угол (-26П/6) .

Но угол (-7П/3)  не лежит между 0 и 2П . Поэтому надо прибавить не 2П,

а  больше , чтобы попасть в промежуток [ 0 ; 2П ] . Подбираем число n .

Если прибавить 3*2П , то получим  

Полученный угол  принадлежит промежутку [ 0; 2П ] .

Замечание.  Если прибавить 2*2П , то не получим угол из

промежутка [ 0;2П ] . Действительно,

 .

То есть можно сообразить, что в числитель к (-26П) надо прибавить число, большее 26П, чтобы получить положительный угол. И соответственно подбирать n .

Если прибавить 4*2П , то получим угол, который больше, чем 2П. Действительно,

То есть n=2 и n=4 не подходит , а n=3 как раз подходит .