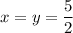Числа x и y положительные, при чем x+y=5. какое найменшее значение может принимать выражение

Другие вопросы по теме Алгебра
Популярные вопросы
- Тест чтение 2 класс конкурс мамонтенок...
1 - Знайдіть дугу, на яку спирається вптсаниф кут, що дорівнює 42°...
1 - Сделай схему предложений 1)снежинки падали с небес в таком случайном беспорядке,...
1 - Шаршынын жарты периметыры табу онын кабыргасы а) 8дм э) а дм...
3 - Бетховен сказал о бахе: «не ручей! море должно быть имя ему». согласны ли...
3 - Сочинение на тему со свинным рылом да в калашный ряд,будьте добры...
2 - Вгороде л. играли вальс; контрабас гудел отрывисто, скрипка неясно заливалась,...
1 - Укажите вариант ответа, в котором правильно определена синтаксическая функция...
2 - Предлагаем игру третий лишний . составьте любую пару слов,обосновав свой...
1 - Какие качества дубровского проявляются при встрече с машей? почему вы так...
1
x + y = 5 отсюда y = 5 - x.
Рассмотрим функцию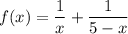
Производная функции: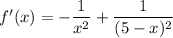 и приравняем ее к нулю.
и приравняем ее к нулю.
(0)____-_____(2.5)____+___(5)___+___
В точке x = 2.5 производная функции меняется знак с (-) на (+), следовательно, x = 2.5 - относительный минимум.
y = 5 - 2.5 = 2.5
ответ: при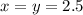 выражение
выражение 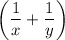 принимает наименьшее значение.
принимает наименьшее значение.
Второй без производной)
Для x,y> 0 применим неравенство Коши
При этом равенство достигает наименьшего значения при