Четыре прямые, нарисованные на координатной плоскости, ограничивают квадрат. Угловой коэффициент одной из них равен 2. Найдите сумму угловых

Question

Алгебра: Четыре прямые, нарисованные на координатной плоскости, ограничивают квадрат. Угловой коэффициент одной из них равен 2. Найдите сумму угловых коэффициентов (представленных в виде целого числа или несократимой дроби) остальных трех.

njjk1 · Answer

y=kx+b - уравнение прямой на координатной плоскости,

где - угловой коэффициент.

1) Известен угловой коэффициент первой прямой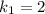 k_1=2 .

2) Противоположная сторона квадрата лежит на прямой, параллельной первой прямой, а необходимым и достаточным условием их параллельности является равенство их угловых коэффициентов.

Получаем:

k_1=k_2=2

3) Две остальные стороны квадрата лежат на прямых, перпендикулярных первой прямой, а для этого необходимо и достаточно, чтобы их угловые были обратны по величине и противоположны по знаку.

Получаем:

$k_3=k_4=-\frac{1}{k_1}=-\frac{1}{2}=-0,5$