1. Алгебра
  2. Четвёртый член арифметической

Четвёртый член арифметической прогрессии равен 8, а двадцатый член равен 40. Найдите первый и шестой члены арифметической прогрессии.

Паралиллепипед Паралиллепипед    3   14.12.2020 12:35    0

Ответы
vikailen vikailen  13.01.2021 12:36
A1=2
a6=12
——————————————
ПОКАЗАТЬ ОТВЕТЫ
alinkarazborova alinkarazborova  13.01.2021 12:36

Для  начала найдем разность арифмитической прогрессии

по формуле :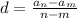d=\frac{a_{n}-a_{m} }{n-m}

an и am это какие та два не последовательных члена арифмитической прогрессии , в нашем случае у нас an=a20 am=a4

d=\frac{40-8}{20-4} =\frac{32}{16} =2

теперь когда известна разность узнаем чему равен первый член прогрессии по формуле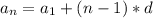a_{n}=a_{1}+(n-1)*d

вместо an подставим уже известный четвертый член арифмитической прогрессии

8 =a_{1} +(4-1)*2

8=a_{1} +6

a_{1} =8-6

a_{1} =2

теперь найдем шестой член прогрессии

по той же формуле

a_{6}=2+(6-1)*2

a_{6}=12

Объяснение:

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
поняття поняття  09.08.2019 06:30
Доказать для всех действительных (x,y)...
DeM12345 DeM12345  08.09.2019 12:30
Проходит ли график функции у=-х+3 через точку b(10 -7)...
vqw80494 vqw80494  08.09.2019 12:30
Найти значение острого угла альфа, если: cos75=cos(90-альфа) вычислить с формулы : cos150 sin135 ctg135 cos120 объясните, как делать это фигню? я вообще ничего не : (...
leeJLZeel leeJLZeel  08.09.2019 12:30
Перевести градусы в радианы, 40, 50, 905 градусов в радианы...
vadimkamazurke vadimkamazurke  08.09.2019 12:30
Докажите что функция y=8x-2 является возрастающей или убывающей...
Dashakrasaveta Dashakrasaveta  08.09.2019 12:30
1.найдите область определения функции y=log(x^2+x+1) y=log(4-x^2) 2.каким соотношением связаны числа m и n, если lg m=1,4153 lg n=3,4153...
Aruzhka001 Aruzhka001  08.09.2019 12:30
Данное выражение запишите в виде числового выражения и найдите его значение: а)разность произведения чисел 5/6 и 0,3 ичисла 1,3 б)частное чисел 2/9 и 4/15 увеличить на 1,2...
artursaripov851 artursaripov851  08.09.2019 12:30
(2√2+5√3)(4√2-√3) . напишите решение подробное,...
Qweres2000 Qweres2000  08.09.2019 12:30
Розставье дужки так, щоб рівність стала тотожністю: х²-2х+1-х²-2х-1=-2...
kirmanova79 kirmanova79  08.09.2019 12:30
Найдите допустимые значения переменной в выражении:...

Популярные вопросы