Через точку А(-2;0) координатной плоскости проведена некоторая прямая, пересекающая график функции у=х² в точках с абсциссами х1 и х2. Найдите значение величины 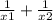
Другие вопросы по теме Алгебра
Популярные вопросы
- Стадии развития с полным преврощением...
3 - Втреугольнике abc угол a на 20% больше угла b, а угол c на 80% меньше угла...
3 - 100 , напишите программу, которая вычисляет среднюю за неделю температуру...
2 - Разделить текст на предложения.маленькая светланка играла в песочнице вдруг...
2 - Сначала суток секунд (n-целое).найти количество полных минут с чала суток....
1 - Вставьте пропущенные буквы раскройте скобки: огл_вление обл_к_титься ост_лб_неть...
3 - Составьте план к расказу васюткино озеро полный план...
3 - (sinx+cosx)^2=1+cosx (sinx-cosx)^2=1+sinx...
1 - Найдите шестой член и сумму шести первых членов арифметической прогрессии(a),...
3 - Які вуглеводні можна одержати гідруванням 2,4-диметилгексену-3?...
1
Объяснение:
Пусть прямая задается уравнением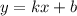
Поскольку прямая проходит через точку , то подставив её координаты в уравнение прямой получим:
, то подставив её координаты в уравнение прямой получим: 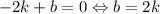
Значит наша прямая имеет вид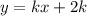
В точках пересечения значения функций должны быть равными
По т. Виета: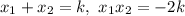 , значит
, значит
P.S.: Тут хорошо бы еще отметить, что поскольку в условии заранее известно, что прямая пересекает параболу в двух точках, то проверять условие наличия корней у квадратного уравнения не требуется. Так же, в последней строчке решения, при сокращении дроби на по идее необходимо убедиться что
по идее необходимо убедиться что 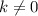 , однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)
, однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)