Через центр окружности x^2+y^2=2x проведена прямая, параллельная прямой x+2y=0 и пересекающая окружность в точках a и b. найдите площадь треугольника aob, где точка о - начало координат

Это уравнение окружности с центром (1;0) и радиусом R = 1.

Пусть общий вид неизвестной прямой y = kx + b. Эта прямая параллельна прямой x + 2y = 0, т.е. у параллельных прямых угловые коэффициенты равны: k = -0.5. Получаем y = -0.5x + b. Известно, что прямая y = -0.5x + b проходит через центр окружности (1;0), т.е., подставляя координаты точки центра окружности, мы найдем коэффициент b

Таким образом, нашли неизвестную прямую y = -0.5x + 0.5 или x + 2y - 1 = 0

Наглядно нарисуем графики и данный треугольник.

Найдем уравнение прямой, проходящей через точку O(0;0) и перпендикулярно прямой x + 2y - 1 = 0.

Прямая, проходящая через точку M(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнением:

Далее найдем координаты точки пересечения двух прямых y = -0.5x + 0.5 и y = 2x.

Точка D имеет координаты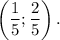 . Расстояние от точки О до точки D:

∠AOB опирается на диаметр AB, следовательно, ∠AOB = 90°, а диаметр окружности в два раза больше радиуса, т.е. AB = 2R = 2 * 1 = 2.

Площадь треугольника AOB:

кв.ед.

ответ: 1/√5 кв. ед..