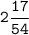Чему равна площадь фигуры ограниченной линиями y=(3x+2)(x-1) .y=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Знайти суму і різницю векторів ā=(0; 1; 2) i c=(-3; 0; 5)...
3 - Как перевести смешанную дробь в десятичную?...
3 - При приготовлении сиропа для пропитки торта необходимо рас- творить в воде массой...
1 - Які заходи з охорони води нині існують та впроваджуються?...
2 - с геометрией Даны числа a, b и c, причем 0 a b c и a,b и c – стороны прямоугольного...
3 - Со словом в котором корень суффикс (к) и окончание (а)...
1 - Якій алгоритмічній конструкції відповідає зображена на малюнку блок схема...
3 - Складіть назви за систематичною номенклатурою...
2 - Zn → FeSO4 → X → ZnO осуществить цепочку...
1 - Дан равнобедренный треугольник abc основание ac равно 4 корня из 2 см медиана ам=...
3
y=(3x+2)(x-1)=3x²-x-2
Это парабола, ветви направлены вверх т.к. старший коэффициент больше нуля. Нули функции:
у=0 это прямая, которая совпадает с ось Ох.
Получается, что
ответ: