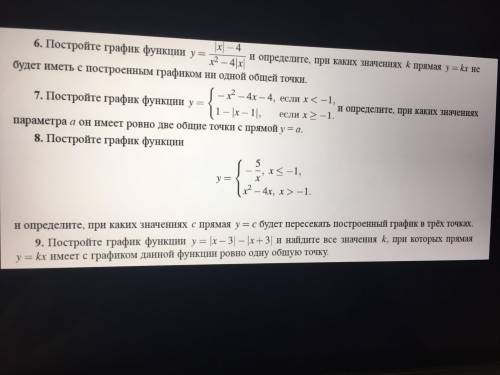
Алгебра: Че-то сделать с функциями, 9 номер, я приложила

Че-то сделать с функциями, 9 номер, я приложила

Ответы

teenwolf18 23.06.2021 23:52

Объяснение:

Нули подмодульных выражений:

х=-3 и х=3

Три промежутка:

1)х≤-3 y=-x+3+x+3; y=6

2)-3<x<3

y=-x+3-x-3; y=-2x

3)x≥3

y=x-3-x-3; y=-6

y=kx

k>-2

Че-то сделать с функциями, 9 номер, я приложила

ПОКАЗАТЬ ОТВЕТЫ

basarbakhtiar 23.06.2021 23:52

Объяснение:

$y = |x - 3| - |x + 3| = ... \\ \small{|x - 3| = \begin{cases} \: x - 3 \: npu \: x \geqslant 3 \\ 3 - x \: npu \: x < 3\end{cases} }\\ \small{ |x + 3| = \begin{cases} \: x + 3 \: npu \: x \geqslant - 3 \\ - x - 3 \: npu \: x < - 3\end{cases} } \\ ... \small{= \begin{cases} - x + 3 - ( - x - 3) \: npu\: \: x < - 3\\ - x + 3 - ( x + 3) \: npu \: \: - 3 \leqslant x < 3 \\ x - 3 - ( x + 3) \: npu \: \: x \geqslant 3 \end{cases} = } \\ \small{= \begin{cases} - x + 3 + x + 3 \: \: \: npu\: \: x \in ( - \infty ; \: - 3)\\ - x + 3 - x - 3 \: npu \: \:x \in [-3;\: 3) \\ x - 3 - x - 3 \: \: \: npu \: \: x \in [3; \:+ ) \end{cases} = } \\ \small{= \begin{cases} \: \: \: 6 \: \: \: \: npu\: \:x \in (- \infty ; \: - 3) \\ - 2x \: \: npu \: \:x \in [-3;\: 3) \\ - 6 \: \: \: \: npu \: \: x \in [3; \:+ \infty ) \end{cases} = } \\$

Как видно из рис., график ф-ии у = kx всегда имеет с графиком рассматриваемой ф-ии общую точку (0;0)

Очевидно, что больше пересечений и совпадений не имеют графики таких функций, которые

1) не пересекают прямые у = 6 и у = -6

2) пересекают прямую у = 6 в т. х>-3

(т.к. и рассматриваемая ф-ия, и ф-ия у = kх + b - нечетные, достаточно рассмотреть пересечение только с одной из прямых у = или у = -6)

1) Такая ф-ия только одна: при k= 0 y = 0

2)Исключив значение k = 0 мы можем записать обратную функцию:

$\begin{cases}y = kx , \\ k≠0 \\ \end{cases} < = x = \frac{y}{k}$

Слова "пересекают прямую у = 6 в т. х>-3" означают, что в обратной ф-ии

при значении у = 6

значение х > -3, или:

$x(y) = \frac{y}{k } \begin{cases} x(6) -3, \\ k≠0 \end{cases} \\ \frac{6}{k} -3 < = k - \frac{6}{3} < = \: \: \\ k - 2 , \: \: \: k≠0 = \\ = k \in \: (-2;0) \cup(0;+ \infty )$