быстрей.
определите характер монотонности!
Другие вопросы по теме Алгебра
Популярные вопросы
- составьте пары предложений с данными чтобы они выступали как разные части...
3 - Что необходимо предпринять, если в процессе растворения соли в воде раствор...
2 - 15. Начните составлять таблицу «Развитие украинской культуры в XVI в.»(в...
3 - Найдите числа на координатной прямой которые накодятся на расстоянии 4 единицы...
1 - Предмет лежить у вертикальній площині як треба посативити плоске дзеркало...
1 - Решите 1 тест. ответ дать вместе с объяснением! Как и что надо делать! 11....
3 - Тест по теме: «Медианы, биссектрисы и высоты треугольника» 1 вариант 1....
2 - ответить на тесты . Даю 100 б...
2 - Можно ли получить из 6 семёрок число 100...
2 - 1.на расчет поступили денежные средства от покупателей 2.выплачена заработная...
3
Обе функции монотонно возрастающие.
Получили, что мЕньшему значению переменной соответствует мЕньшее значение функции, и наоборот, бОльшему значению переменной соответствует бОльшее значение функции. Значит функция возрастающая .
Знак выражения получили (+) , так как произведение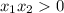 в силу того, что гиперболу рассматриваем на двух промежутках при
в силу того, что гиперболу рассматриваем на двух промежутках при 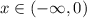 и при
и при 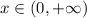 , где
, где 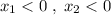 и
и 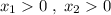 .
.
Получили, что бОльшему значению переменной соответствует бОльшему значение функции, и наоборот, мЕньшему значению переменной соответствует мЕньшему значение функции. Значит функция возрастающая .