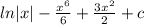Буду очень благодарен, если решите
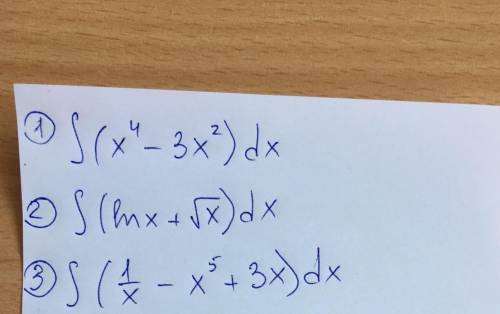
Другие вопросы по теме Алгебра
Популярные вопросы
- Постройте граф,отображающий отношения между следующими понятиями: информационные...
1 - Сочинение на тему: -это развлечение или размышление?...
1 - Вся семья на выходных поехали за грибами. сын нашёл 37 боровиков, мама собрала...
1 - Эссе на тему казахстан на карте мира...
3 - Решите уравнение а) x - 6\11 +4\11 б) 17/25 - ( 3/25+x)=8/25...
3 - 10,7,49и70. составте пропорцию из данных чисел:...
2 - Составить 4 сложных предложения без союзов и с саюзами (и,что,потому что)...
1 - Фонетический разбор слова грядка второй и четвертый звук...
1 - Существует некоторое число, которое делится на 5 и 9 одновременно. определи...
1 - Электричка едет со скоростью 60 миль в час. если есть ветер 30 миль в час,...
1
1.
2.
берем по частям:
Получаем:
3.
Объяснение:
1)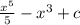
2)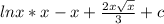
3)