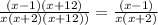Братцы, выручайте! еще одна дробь. .
Другие вопросы по теме Алгебра
Популярные вопросы
- Очі-органи зору Рака річкового мають особливості будови?...
1 - Tg(x+y)-tgx-tgy/tgxtg(x+y)=tgyтепе-теңдікті дәлелде ( докажи уровнение)...
3 - очень надо Запишите произведение одинаковых множителей в разложении числа...
1 - «Күлтегін» жырының басқа жырлардан айырмашылығы неде?...
2 - Було 10 Яблокі пять яблоків забрали Скільки лишилося яблоків...
1 - Match the words with their defipetions...
2 - 1-тапсырма. Ребусты шешіп, жасырылған сөзге қатысты ой бөлісіңдер 6класс...
1 - Сипаи -Каковы последствия английской колонизации Индии? 1.2.3....
3 - Задание 1 1. Прочитайте два текста.2. Назовите основную мысль текстов.3....
1 - 1. Мықты жігіт неге ағаштың басына шығып кетті?2. Ауру жігіт неге жерге...
2
Решим два дискриминанта:
x²+11x-12=0
a=1 b=11 c=-12
D=b²-4ac=> 11²-4*1*(-12) = 121+48 = 169 = 13² => 2 корня
x =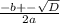
x₁ =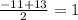
x₂ =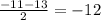
x²+14x+24=0
a=1 b=14 c=24
D=b²-4ac=> 14²-4*1*24 = 196-96 = 100 = 10² => 2 корня
x =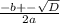
x₁ =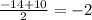
x₂ =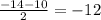
Получаем: