без игнора умоляю

1) запишите с пи в радианах углы равнобедренного треугольника;
2) запишите с пи в радианах углы равностороннего треугольника;
3) запишите с пи в радианах углы прямоугольника

    1)   π / 4,   π / 4,   π / 2;  

    2)   π / 3,   π / 3,   π / 3;  

    3)   π / 2,   π / 2,   π / 2,   π / 2.  

1 ) Углы равнобедренного прямоугольного треугольника равны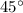 , 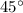и 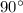(если треугольник "прямоугольный", то в нем есть угол в 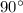, а если к тому же равнобедренный, то его два оставшихся угла равны по ).

, откуда каждый из углов треугольника в равен радиан.

, или же - это радиан.

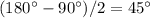2 ) Сумма углов треугольника равна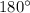 или 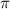радианам. Если треугольник равносторонний (название говорит само за себя), то все его три угла равны. Иначе говоря, каждый из них равен 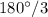(что равно 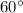) или же 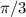радиан.

3 ) Все углы прямоугольника (таковых имеется четыре) равны. А сумма углов прямоугольника, как и любого четырехугольника, равна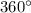 , что равняется 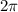радиан. Отсюда несложно сделать вывод, что каждый из углов прямоугольника равен 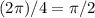радиан.

Или можно вспомнить, что с углом в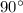 мы уже встречались в первом пункте задачи: как было выяснено, он соответствует 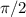радиан.