Берілген өрнектердің тепе-тең болатынын дәлелдеңдер 


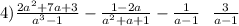
Другие вопросы по теме Алгебра
Популярные вопросы
- Гуманистические идеи в романе капитанская дочка. сочинение...
3 - Вгосударстве z все уважают закон и ему подчиняются. какая дополнительная информация...
3 - Из каких основных частей состояла территория средневекового европейского города?...
2 - Вмедном стакане массой 400 г находится 500 г воды при 40°c, в воду бросили кусок...
1 - Как проявляется в кубок 1)героизм 2)рыцарство 3)...
3 - Решить пример . 1.) 8,5× ( 16,7 - 13,97 ) + 4 3/8 ÷ 1 1/6 = 2.) (2 2/15 + 3...
2 - Каким предстаёт автор в стихотворениях парус и листок ? что мы узнаем о его...
1 - По словарю в конце учебника выясните, что такое конституция. поскольку известно,...
1 - Две группы велосипедистов поехали от турбазы в противоположных направлениях....
1 - Доказать методом от противного. через точку, не лежащую на прямой, проходит...
1
Объяснение:
1)
2)
3)
4)