1. Алгебра
  2. B1+b5=34, b2+b6=68. какой номер

B1+b5=34, b2+b6=68. какой номер имеет член, равный 128? ​

Великолепныйум Великолепныйум    3   11.04.2019 00:15    0

Ответы
sergey1234567890f sergey1234567890f  29.05.2020 06:09

Я так понимаю, речь идёт о геометрической прогрессии?

b_1+b_1q^4=34\\b_1q+b_1q^5=68\\\\\\b_1(1+q^4)=34\\b_1q(1+q^4)=68

Очевидно, что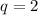 q=2. Вернёмся к первому уравнению, чтобы найти b_1:

b_1+b_1q^4=34\\b_1(1+q^4)=34\\b_1(1+2^4)=34\\b_1 \cdot 17=34\\b_1=2

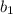Теперь найдём номер члена, равного 128:

b_1q^{n-1}=128\\2 \cdot 2^{n-1}=128\\2^n=128\\2^n=2^7\\n=7

ответ: седьмой.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
syuzannsckorny syuzannsckorny  16.02.2020 00:34
Виконайте множення ОЧЕНЬ НУЖНО...
hihilaim hihilaim  16.02.2020 00:14
Знайдіть найменший додатний корінь рівняння: 1) cos(2x-pi/4)=sqrt2/2 2)sin(x/2+pi/6)=1/2...
ваняшка ваняшка  28.05.2020 19:33
Решите систему неравенств: 2х-5 3 4х+3 0 Заранее...
l0958626315 l0958626315  27.05.2020 19:33
1. За нового князя на люботинських земляхА сусіди зазіхали на прикордонні поселення Б запанувало затишшяВ затівалися баталії Гпід час ловів Мисливці тoлoчили жита​...
treezykilla treezykilla  28.05.2020 19:33
Визначити маси розчинів солі з масовими частками речовин 15% та 75% , необхідні для приготування 600 г розчину з масовою часткою 35%....
kamil281102 kamil281102  27.05.2020 19:33
решить 1,2,5 пожайлуста,остальное решили решить 1,2,5 пожайлуста,остальное решили >...
ДарьяOver ДарьяOver  27.05.2020 19:33
Складіть квадравтне рівняння,корені якого більші за відповідні рівняння x²+5х-7=0 на 1...
varvaralikhtsr varvaralikhtsr  27.05.2020 19:33
7 класс, заранее класс, заранее...
секрет93 секрет93  27.05.2020 19:33
Воды израсходовали на полив огурцов за 3 дня хватило бы на полив помидоров в течение недели. Всего на полив этих овощей за 8 дней ушло 9,6 тонн воды. сколько воды...
memasov memasov  27.05.2020 19:33
Для функции f(x) = х ^+ 3 sin x найдите какую-ни­будь первообразную, график которой проходит через точку А (2 ;0)...

Популярные вопросы