1. Алгебра
  2. Арифметическая прогрессия:

Арифметическая прогрессия: 1)а1=5, d=-7. найдите а30. 2) а7=22, а9=32. найдите d,а1. 3)а1=-2, d=9.найдите s7. 4)(аn): 7; 5; 3; арифметическая прогрессия. 5) каким будет номер члена арифметической прогрессии равной 53, если а1=-4, d=3. , напишите подробно как решать.

ипоопан ипоопан    1   18.05.2019 07:40    58

Ответы
kostaKOSTAkosta kostaKOSTAkosta  11.06.2020 14:00

1) По формуле n-го члена арифметической прогрессии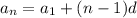 a_n=a_1+(n-1)d, вычислим тридцатый член этой прогрессии

a_{30}=a_1+29d=5+29\cdot(-7)=-198


ответ: -198.


2) Снова же используем формулу n-го члена арифметической прогрессии:

a_{9}=a_1+8d=\underbrace{a_1+6d}_{a_7}+2d=a_7+2d\\ \\ d=\dfrac{a_9-a_7}{2}=\dfrac{32-22}{2}=5\\ \\ a_1=a_9-8d=32-8\cdot5=-8


3) Используем формулу суммы первых n членов арифметической прогрессии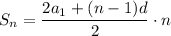 S_n=\dfrac{2a_1+(n-1)d}{2}\cdot n


S_7=\dfrac{2a_1+6d}{2}\cdot7=7\cdot(a_1+3d)=7\cdot(-2+3\cdot9)=175


ответ: 175


4) Условие неполное.


5) Используем формулу n-го члена арифметической прогрессии

a_n=a_1+(n-1)d\\ 53=-4+3(n-1)\\ 57=3(n-1)~~|:3\\ 19=n-1\\ n=20


20 член арифметической прогрессии равен 53.


ответ: 20.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
daniilbesperst daniilbesperst  13.09.2021 04:32
решите уравнение и объясните решение...
Mirajanesan Mirajanesan  13.09.2021 04:35
Функциясы берілген y=y=x²-10x+21...
ПОЗИТИВЧИК750 ПОЗИТИВЧИК750  13.09.2021 04:37
Побудувати графік функції у=-2х +3....
sadlyuda sadlyuda  13.09.2021 04:41
Приведите подобные члены многочлена 3²x-5³x +3-4x³-x²....
ggf6fr ggf6fr  13.09.2021 04:42
14 7/5 - 3 3/23 • 23/27 - 1 1/5 • 1/6...
mumusinka mumusinka  13.09.2021 04:43
решить. Распишите как решать и первый тоже решите....
extysq3000 extysq3000  13.09.2021 04:44
Реши неравенство и запиши ответ в виде числового интервала: 4x−4≤52−4x. x∈ _ _; _ _ (Вводи скобки отдельно от чисел; если нужно написать −∞, пиши −Б; если +∞ — пиши...
умник202323 умник202323  14.05.2020 19:53
M(1-n)-(n-1). Разложить на множители...
Евгеха001 Евгеха001  14.05.2020 19:53
Двоє робітників виготовили 657 деталей при чому перший виготовив на 63 деталі більше скільки деталей виготовив кожний робітник. Зробіть будь ласка системою....
Skripp Skripp  14.05.2020 19:53
1°. Чи є число 8 коренем рівняння: 1) х + 3 = 10; 2) 48 : х = 6? с обьеснением...

Популярные вопросы