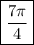Arccos(cosx)=x-3π/2
найти значение x
Другие вопросы по теме Алгебра
Популярные вопросы
- Докажите, что четной является функция:а) р (x)=x⁴;б) p(x) = — 3х⁶....
3 - В 250 г 5%-ого раствора CuSO4 растворимости ещё 125 г СuSO4. Вычесть массовую...
3 - Зачем нужно воображение? Расставь знаки препинания в предложении с прямой речью....
1 - A Across3 1_ to hip hop music with my friends.4 We _ a big party every year.5...
1 - У Кати были матрёшки. 4 матрёшки она собрали убрала в сумочку, а двеоставила....
3 - УМОЛЯЮ Нужен ответ, который 100% верный....
2 - как удалить вопрос на этой платформе где находится корзина киньте скрин с корзиной...
2 - Визнач,чому дорівнює температура повітря на вершині Кіліманджаро (Африка),якщо...
2 - Какова роль причастных оборотов в данном тексте. Утром Ленька проводил нас...
3 - Сделай вывод, на какие вопросы отвечают одушевленные и неодушевленные имена...
2
Область значений функции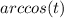 это
это ![[0;\pi]](/tpl/images/0742/6095/4b0a1.png)
Значит,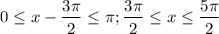
Ограничение на x есть.
Теперь чтобы решить это добро, возьмем косинус от левой и от правой части.
Так что применим это сюда:
Проверим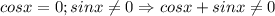 , значит, мы можем смело поделить на
, значит, мы можем смело поделить на 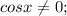
Получим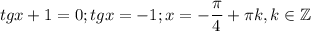
Теперь надо вернуться к ограничению:
Из целых чисел на этом отрезке есть только k=2
ответ: