1. Алгебра
  2. Анализ граница lim x→0 (8x^2)/(sin^2

Анализ граница lim x→0 (8x^2)/(sin^2 (5x))

KusokKirpicha KusokKirpicha    1   06.09.2019 07:20    0

Ответы
Глебюдон Глебюдон  16.08.2020 10:26
Неопределённость 0/0. В данном случае раскрытие неопределённости сведём к первому замечательному пределу.

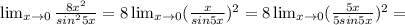
\lim_{x \to \inft0} \frac{8 x^{2} }{sin^{2} 5x} =8 \lim_{x \to \inft0} (\frac{x}{sin 5x} )^{2}=8 \lim_{x \to \inft0} (\frac{5x}{5sin 5x} )^{2}=

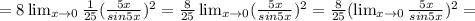
=8 \lim_{x \to \inft0} \frac{1}{25} (\frac{5x}{sin 5x} )^{2}= \frac{8}{25} \lim_{x \to \inft0} (\frac{5x}{sin 5x} )^{2}=\frac{8}{25} (\lim_{x \to \inft0} \frac{5x}{sin 5x} )^{2}=

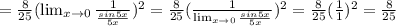
=\frac{8}{25} (\lim_{x \to \inft0} \frac{1}{ \frac{sin 5x}{5x}})^{2}=\frac{8}{25} (\frac{1}{\lim_{x \to \inft0} \frac{sin 5x}{5x}})^{2}=\frac{8}{25} (\frac{1}{1} )^2=\frac{8}{25}
ПОКАЗАТЬ ОТВЕТЫ
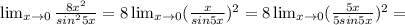
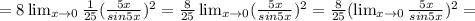
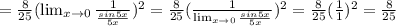
Другие вопросы по теме Алгебра
солнвшко солнвшко  03.10.2019 02:50
У=2х-3 является ли линейной функция...
одиннадцать1 одиннадцать1  03.10.2019 02:50
У=7-9х является ли линейной функция...
meshiydima meshiydima  03.10.2019 02:50
Постройте таблицы для функций: y=3x. y=-0.5x 15...
20031003veronika 20031003veronika  17.10.2020 15:35
с Алгеброй построения графиков функции !...
vabimGogolev vabimGogolev  17.10.2020 15:35
Вынеси множитель из-под знака корня:3/8 ^128 ?! Как решить? ​...
cherru1 cherru1  17.10.2020 15:35
При каких значениях x имеет смысл...
Anna66613 Anna66613  17.10.2020 15:30
Запишите число в стандартном виде 52 320000​...
Holmes9 Holmes9  17.10.2020 15:01
в8 степени нужно представить в виде километра​...
andreyyurinp06nhg andreyyurinp06nhg  17.10.2020 15:01
Представьте числа в виде √а и расположите их в порядке убывания: -2√5; -5√3; -3√11...
melisa9999 melisa9999  17.10.2020 15:01
Нужен просто ответ из этих номеров Стандартная форма номера 6720000: [1]A. 0,672∙10^(-7)B. 6,72∙10^4C. 67,2∙10^5D.6,72∙10^6Е. 627∙10^7...

Популярные вопросы