Алгебра! Только нужно расписать чтобы было понятно
Другие вопросы по теме Алгебра
Популярные вопросы
- Света, Маша и Оля разделили между собой 80 конфет. Света заметила, что если...
3 - 7.Как относился к охоте отец автора?Найдите и запишите отрывок.И.Тургенев...
1 - ПАМАГИТЕЕ С РОЧНОО Запиши десятичную дробь в виде смешанного числа. В результате...
2 - биология 7 класс №1Дайте общую характеристику типа членистоногие по следующим...
2 - Найти лирические отступления размышления факты биографии в Руслан и Людмила...
2 - Два туристи вийшли з міста A в місто B одночасно. Перший турист кожен кілометр...
2 - Опишите географическое положение западно-сибирской равнины план описания...
1 - На каком явлении основано зрение...
1 - 3. Оқылым мәтінінен тірек сөздерді анықтаңдар. Оларды сан есімдермен тіркестіріп,...
3 - Самостоятелытая работа Задание 2. Постройте на координатной плоссоедините...
1
[1]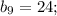
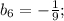
Формула n-ого члена геометрической прогрессии: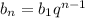
Распишем для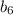 и
и 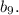
Составляем систему, чтобы выразить q (знаменатель геом.пр.) :
Решаем:
[2]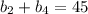
Составим и решим систему, чтобы получить значения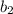 и
и 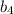 :
:
Получаем корни:
Находим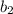 :
:
Так как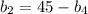 , то:
, то:
Заметим: что в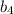 , что в
, что в 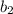 - выходят одинаковые значения (36 и 9). От перестановки слагаемых сумма не меняется. Поскольку у нас возрастающая прогрессия, возьмем за
- выходят одинаковые значения (36 и 9). От перестановки слагаемых сумма не меняется. Поскольку у нас возрастающая прогрессия, возьмем за 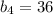 , а за
, а за 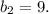
Чтобы найти первый член прогрессии, находим ещё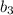 и
и 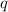 :
:
Формула: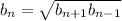
Решение: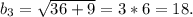
И теперь мы можем с формулы n-ого члена геометрической прогрессии: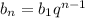 , вывести первый член прогрессии. Значит:
, вывести первый член прогрессии. Значит: