Алгебра. Решите биквадратное уравнение.

Другие вопросы по теме Алгебра
Популярные вопросы
- Через точку d , лежащую на стороне ac тругольника abc...
3 - 1. в одной коробке 12 карандашей. число карандашей в этой коробке относится к...
1 - Sam asked his friend, do you like the company you work with? = sam asked his...
3 - Скласти діалог 8-10 реплік між друзями про нову комп ютерну гру з словами іншомовного...
2 - Найди лишнее животное заяц волк еж собака лиса...
3 - Составьте слова из пяти звуков, которые здесь описаны.1.звонкий,парный звук ф.2...
1 - Надо придумать загадку про питомца (кот)....
1 - Доказательство о шарообразности земли...
3 - 99 ! 2b. a classic read 1. translate the words. play snowball: use these words...
1 - Какое явление доказывает беспорядочность движения частиц?...
1
x⁴ + 3x² - 7 = 0,
Делаем замену переменной x² = t, тогда x⁴ = (x²)² = t²,
t ≥ 0.
t² + 3t - 7 = 0,
D = 3² - 4·1·(-7) = 9 + 28 = 37,
1)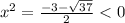
здесь решений нет, т.к. x² ≥ 0.
2)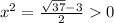
ответ.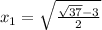
или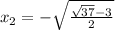 .
.